4008. Binomial coefficients
Gunnar is
quite an elderly and forgetful researcher. Currently, he is writing a paper on
security in social networks that involves some combinatorics. He developed a
program to calculate binomial coefficients to assist him in verifying some of
his calculations.
The binomial
coefficient 
is a number defined by
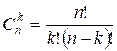
where n and k are non-negative integers.
Gunnar uses his
program to calculate and obtains a number m as a result. Unfortunately, being
forgetful, he forgot the numbers of n
and k he used as input. These two
numbers were the result of lengthy computations and were written on one of the many
sheets scattered across his desk. Instead of searching through the papers, he decided
to reconstruct the numbers n and k from the obtained
answer. Can you help him find all possible values?
Input. The first
line contains the number of test cases, at most 100. Each test is given in
a single line and contains an integer m (2 ≤ m ≤ 1015) – the result
of the Gunnar’s program.
Output. For each
test, print two lines. The first line should contain the number of ways to
express m using the binomial coefficient. The second line should
contain all pairs (n, k) such that = m. Pairs should be
sorted in increasing order of n, and in case of equality,
in increasing order of k. The output format
of pairs is given in the example.
|
Sample
input |
Sample
output |
|
2 2 15 |
1 (2,1) 4 (6,2) (6,4)
(15,1) (15,14) |
SOLUTION
combinatorics – binomial
coefficient – binary search
Algorithm analysis
If = m, then 
= m. It is sufficient to find the solution for k ≤ n / 2 and,
along with the pair (k,
n), also print the pair (k, n
– k). For k = n / 2 these
two pairs coincide.
Let p be the smallest number for which 
> m. Then it is obvious that 0 ≤ k < p.
Choose k such that 
≤ m and consider the function f(n) = . Then for 2k ≤ n ≤ m,
the function f(n) is monotonically increasing. Therefore,
you can solve the equation f(n) = m by binary
search.
To solve the
problem, one should iterate over the values of k (0 ≤ k < p), and for each such k, solve the
equation = m relatively n with binary search.
The found value of n must be an integer.
Example
Consider the
equation = 3003. Given that 
= 924 and 
= 3432, it is sufficient to iterate over 0
≤ k ≤ 6.
Let k = 2, consider the equation 
= 3003 or 
, n * (n – 1) = 6006. By binary search in the
interval 4 ≤ n ≤ 3003, we find an integer
solution n = 78. Since n ≠ 2*k, we
have two solutions: 
= 
= 3003.
Algorithm realization
Store the
required pairs in the vector of pairs res.
vector<pair<long long,long long> >
res;
The Cnk function computes the
value of binomial coefficient 
.
long long
Cnk(long long
n, long long k)
{
long long i, Res = 1;
if (k > n
- k) k = n - k;
for(i = 1; i
<= k; i++)
{
If at the next iteration the result exceeds m (we are searching for a solution
to the equation = m), then stop computations. Exiting the function at this point avoids overflow.
if (1.0 *
Res * (n - i + 1) / i > m) return m + 1;
Res = Res * (n - i + 1) / i;
}
return Res;
}
The main part of the program. Read the input data.
scanf("%d",&tests);
while (tests--)
{
res.clear();
scanf("%lld",&m);
Iterate over the values of k from 0 until ≤ m.
for(k = 0;
Cnk(2*k,k) <= m; k++)
{
Find the value of n (2k ≤ n ≤ m) using binary search.
long long lo = 2*k, hi = m;
while (lo
< hi)
{
long long n = (lo + hi) / 2;
if
(Cnk(n,k) < m) lo = n + 1; else hi = n;
}
If 
= m, then a solution is found. Include one or two pairs of solutions in the
result.
if
(Cnk(lo,k) == m)
{
res.push_back(make_pair(lo,k));
if (lo !=
2*k)
res.push_back(make_pair(lo,lo - k));
}
}
Sort the pairs.
sort(res.begin(),res.end());
Print the answer – the number of found pairs and the pairs themselves.
printf("%d\n",res.size());
for(i = 0; i
< res.size(); i++)
printf("(%lld,%lld)
", res[i].first,res[i].second);
printf("\n");
}
Python realization
The Cnk function computes the
value of binomial coefficient .
def Cnk(n, k):
Res = 1
if k > n - k:
k = n – k
for i in range(1, k + 1):
If at the next iteration the result exceeds m (we are searching for a solution
to the equation = m), then stop computations. Exiting the function at this point avoids overflow.
if Res * (n - i + 1) // i > m:
return m + 1
Res = Res * (n - i + 1) // i
return Res
The main part of the program. Read the input data.
tests = int(input())
for _ in range(tests):
res = []
m
= int(input())
Iterate over the values of k from 0 until ≤ m.
k
= 0
while Cnk(2 * k, k) <= m:
Find the value of n (2k ≤ n ≤ m) using binary search.
lo, hi = 2 * k, m
while lo <
hi:
n = (lo + hi) // 2
if Cnk(n, k) < m:
lo = n + 1
else:
hi = n
If = m, then a solution is found. Include one or two pairs of solutions in the
result.
if Cnk(lo, k) == m:
res.append((lo, k))
if lo != 2 * k:
res.append((lo, lo - k))
k += 1
Sort the pairs.
res.sort()
Print the answer – the number of found pairs and the pairs themselves.
print(len(res))
for item in res:
print(f"({item[0]},{item[1]})", end="
")
print()